Video from my YouTube channel

Subscribe to My You tube channel

Poisson's ratio

By -
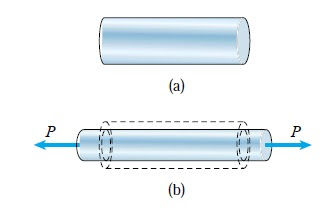
if we stretch a rubber band. the length of the rubber will increase. on the other hand, the diameter will decrease. increase in length represents the axial strain. the decrease in diameter represents the lateral contraction. if we applied a uniaxial tension load for materials such as prismatic steel bar. tension load will cause axial strain and lateral strain normal to the direction of axial load. the lateral and axial strain will be proportional if the applied stress within the elastic region. for steel stress within the elastic region, the amount of lateral strain will be small and not visible. figure no:1 illustrating the concept. figure 1-a shows a prismatic bar prior to loading. figure 1-b shows the bar after loading. we can notice the increase of bar length(axial strain) and the decrease of bar diameter(lateral contraction)
Figure 1






ν=-(ε'/ε)

where 
ν=is the Poisson's ratio
ε'=is the lateral strain
ε=is the axial strain

the minus sign is added to compensate for the fact that axial and lateral strain is opposite in direction always. if we compressed the bar. the opposite will occur. if the Poisson's ratio for the material is known. we can use the equation above to obtain the axial strain if the lateral strain is known and vice versa. the above equation applicable only if uniaxial stress is applied in the axial direction. Table showing the value of Poisson's ratio for a group of materials

Table 1




Comments

Post a Comment

Videos from My Youtube channel

Popular posts from this blog

Pile cap

By -
Image
Pile cap used to transfer the loads from superstructure to the piling. The pile cap is thick concrete mat rests on piles. It is part of the foundation and used to distribute the loads over the piles. Piles used when the soil bearing is not enough to carry loads of the structure. Figure 1  construction management: concrete construction bridge construction:How to become a bridge engineer Pile cap construction procedure Excavation around piles: After 7 days of the casting of the pile the concrete will gain approximately, 70% of it is compressive strength. The soil around piles will be removed to the required levels and dimension that allows construction of the pile cap. A step shall be made if the excavation is more than 1.5 m to prevent soil collapse. Figure 2 Pile head cutting: Concrete will be removed up to cut off level. If concrete under the cut off level is unsound. It shall be removed, and the pile will be repaired...
Read more

prestressing equipment

By -
Image
Jacks are essential tools in prestressing operations and are used to apply tension to strands within tendons. There are two main types of jacks: A. Mono-Strand Jack A mono-strand jack is primarily used in building construction, where tendons typically consist of a small number of strands (usually 3 to 4). This type of jack is designed to stress each strand individually, ensuring precise control over the tensioning process. Since buildings generally have shorter tendons compared to bridges, stressing strands one by one is a practical and efficient approach in this context. construction management: concrete construction bridge construction:How to become a bridge engineer B. Multi strands jack:  In bridge construction, where tendons contain a significantly larger number of strands, using a mono-strand jack would be impractical. Stressing strands one by one in such cases would not only be time-consuming but also increase the risk of strand entrapment. Ther...
Read more

Bridge Diaphragm

By -
Image
The main function of diaphragms is to provide a stiffening effect to deck slab in case bridge webs are not situated directly on top of bearings. Therefore, diaphragms may not be necessary in case bridge bearings are placed directly under the webs because loads in bridge decks can be directly transferred to the bearings.On the other hand, diaphragms also help to improve the load-sharing characteristics of bridges. Diaphragms also contribute to the provision of torsional restraint to the bridge deck. Diaphragm will be used also to resist stresses that occurs during the post-tensioning process. Post-tensioning hardware are casted inside the diaphragm. Figure 1 construction management: concrete construction bridge construction:How to become a bridge engineer Types of diaphragm: Diaphragm at the span end: this type of diaphragms will be located between two bridge spans or at the bridge abutments. Expansion joints will be used to connect bridge spans. This ...
Read more

Repairing of concrete bulging

By -
Image
Improper designing and installation of formwork for a concrete member can result in concrete Bulging. During the placing and compacting of concrete, forms may deflect largely in the weak areas. The deflection of forms will cause concrete to expand at this location, and this known as concrete Bulging. Concrete Bulging will spoil the appearance of a concrete member. Therefore we should always ensure that the forms are appropriately installed, and it is sufficiently supported to resist the concrete during placing and compacting. Bulging should be repaired in case we couldn't avoid it. The solution of concrete Bulging, offset, or surface irregularities are surface grinding. However, excessive surface grinding can weaken the concrete.  Figure 1 If the bulging or surface irregularities are small, grinding of concrete surface will be sufficient to remove surface irregularities. If the Bulging of concrete is significant, then the concrete should be chipped, and the surface...
Read more

Binding wire for steel reinforcement

By -
Image
  Binding wires are used to tie steel bars together. These wires are playing a significant role in maintaining the reinforcement stability and rigidity. Wires are used to tie the steel bars at intersections points. By tying the steel bars together, we ensure that the steel bars will not move from their locations during construction or during the time of concreting. In slabs, binding wires are used to tie longitudinal and transverse bars together. In columns, it is used to tie vertical bars with stirrups.   Figure 1 There are various types of binding wires such as  Black annealed baling wire, Stainless Steel Binding Wire, and PVC coated binding wires.  Black annealed baling wire used to tie black steel. The popular size for black wire ranges from 16 to 22 gauges. Stainless steel binding wires are used to bind stainless steel reinforcement. Stainless steel reinforcement is used in a harsh environment where the black steel gets rusted quickly. Therefore, stainless ...
Read more

Chamfers for concrete structures

By -
Image
In general, the edges of concrete members are chamfered. Usually during the process of installing forms for a structural member such as pile cap, a chamfer a PVC chamfer as shown in figure no:1 installed at the edges of the structural members. These chamfers will form smooth slanted edges, as shown in figure no:2. The size of chamfers can be 20x20mm or more as shown on the contract drawing. The PVC chamfer fixed to forms by nails. We should ensure that the PVC chamfer fixed in their correct locations, and we should ensure that the PVC chamfer is straight and not moving up or down. Checking the alignment and location of PVC chamfer is important, so the chamfered concrete edge will have a good appearance after the form’s removal.  Figure 1 Figure 2 Chamfering the concrete edges done for many reasons such as aesthetics, some suggesting that the chamfering of concrete edges done for safety to reduce the damage of objects due to impact with sharp concrete edges. Actually, ...
Read more

Flakiness Index and Elongation Index of Coarse Aggregates

By -
Image
Flaky and elongated aggregates can adversely affect concrete. Flaky and elongated aggregates are difficult to compact. Therefore using flaky and elongated aggregates will reduce concrete workability, which required more amount of water to produce a workable mix. Increasing water content will reduce concrete strength and durability. Moreover, these aggregates are not robust, which leads to lowering concrete strength. Figure 1 construction management: concrete construction bridge construction:How to become a bridge engineer The Flakiness Index of aggregates is the percentage by weight of particles whose least dimension (thickness) is less than three- fifths (0.6times) of their mean dimension. This test does not apply to sizes smaller than 6.3mm. The Elongation index of an aggregate is the percentage by weight of particles whose greatest dimension (length) is greater than nine-fifths (1.8times) their mean dimension. Flakiness and elongation tests ar...
Read more

Structural design of road pavement

By -
Image
  Designing efficient and durable roads starts with understanding one key factor: traffic. Traffic analysis provides engineers with essential data that directly influences decisions about road width, pavement thickness, and overall design. In this blog, we’ll walk through the fundamental steps of traffic analysis, from traffic surveys to axle load studies, and how each component contributes to building roads that last. watch the full course from here 1. Traffic Analysis The amount and type of traffic a road will carry play a crucial role in pavement design. Roads with heavier traffic flows require not only wider carriageways but also thicker pavements to withstand the higher load repetitions. To estimate how much load a road will bear over its design life, engineers need to conduct a traffic survey . This survey helps assess current traffic volumes and project future trends, giving us a clearer picture of what the pavement needs to endure. 1.1 Traffic Surveys: Gat...
Read more

Driven piles

By -
Image
Driven piles have been used widely as a foundation for different structures. In this type of foundation. Piles are driven to soil mechanically using a hammer. There are enormous types of driven piles. construction management: concrete construction bridge construction:How to become a bridge engineer  Steel H Piles Section of H-pile consists of flange and web, as shown in figure no:1. They are driven using a high impact hammer, and the likelihood of pile damage is low. H-piles resists the loads through skin friction or end bearing or both. Since the displacement of soil is minimal, this type of piles can be driven into dense granular soil or stiff clay layers. Although some problem during driving may arise. Plugging is one of them. After driving the pile to a certain level. soils will adhere to pile web and between the flange creating a closed end. This will change the pile to displaced pile and complicate pile driving. H-piles should be protect...
Read more

stress-strain diagram for aluminium alloy and rubber

By -
Image
figure no:1 showing the stress-strain diagram for aluminum alloy. we can notice from the stress-stress diagram that aluminum has a considerable ductility. despite the absence of explicit yield point as in structural steel . the initial portion of the stress-strain curve is linear with a recognizable proportional limit. the proportional limit for aluminum alloy ranges from 70 to 410 Mpa (10 to 60 Ksi). aluminum alloy undergoes large strain before failure. ultimate stress ranges from 140 to 550 Mpa (20 to 80 Ksi). construction management: concrete construction bridge construction:How to become a bridge engineer Figure-1 Yield stress for aluminum alloy can be determined by drawing offset line parrel to the linear portion of the stress-strain curve. the straight line offset by a standard strain such as 0.002. the intersection point with the stress-strain curve is the point of yield stress. figure no:2 illustrates the concept of offset method. yield stress acquire...
Read more