Video from my YouTube channel

Subscribe to My You tube channel

Change in length for a bar with continuously varying load or dimensions

By -
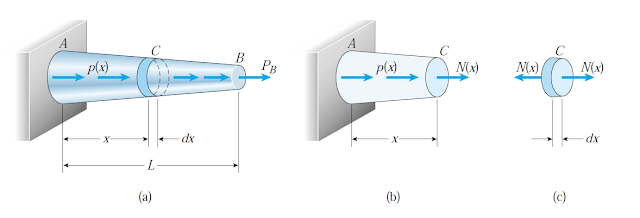
sometimes the axial force and the cross-section area varies along the length of the bar. for this case the equation δ=(PL)/(AE) will not be applicable ,  figure 1 shows a bar with continuously varying load and cross-section area along the length L, for P(x) acting at point A and varying along the length of the bar with force of PB at point B. the force acting along the bar is function of distance (unit of pound per inch or newton per meter). A distributed axial load may be produced by such factors as centrifugal forces, friction forces, or the weight of a bar hanging in a vertical position.






Figure 1









To compute the change of length for this case, we should integrate the change in length of a  differential element of the bar and then integrate over the length of the bar. in general the force is the function of x(change in length) as shown in figure b, the cross-section area A(X) also function of X, we should derive the relation of A as a function of X then use the equation below to calculate the change in length of bar.

dδ=(N(X)*dx)/(A(X)*EA)



Example (click here)




Comments

Post a Comment

Videos from My Youtube channel

Popular posts from this blog

Binding wire for steel reinforcement

By -
Image
  Binding wires are used to tie steel bars together. These wires are playing a significant role in maintaining the reinforcement stability and rigidity. Wires are used to tie the steel bars at intersections points. By tying the steel bars together, we ensure that the steel bars will not move from their locations during construction or during the time of concreting. In slabs, binding wires are used to tie longitudinal and transverse bars together. In columns, it is used to tie vertical bars with stirrups.   Figure 1 There are various types of binding wires such as  Black annealed baling wire, Stainless Steel Binding Wire, and PVC coated binding wires.  Black annealed baling wire used to tie black steel. The popular size for black wire ranges from 16 to 22 gauges. Stainless steel binding wires are used to bind stainless steel reinforcement. Stainless steel reinforcement is used in a harsh environment where the black steel gets rusted quickly. Therefore, stainless ...
Read more

Rebar Splicing and Overlapping — ACI 318-19 Requirements Explained

By -
Image
Reinforcement splicing or overlapping is a fundamental requirement in reinforced concrete structures. Because reinforcement bars (rebars) are manufactured in limited standard lengths—typically 12 m —it becomes necessary to splice or overlap them to achieve the required continuity in structural members. The main purpose of a splice is to ensure smooth stress transfer between adjacent bars through the surrounding concrete. The overlap length, commonly known as the splice length , must be long enough to safely transfer the tensile stresses from steel to concrete without causing bond failure. It is recommended to avoid splicing in high-stress zones such as areas of maximum moment, and to stagger the splices to prevent congestion and reduce stress concentration. The ACI 318-19 providing the following recommendatin and requirement for the lap splicing: 1. Splice Limitation by Bar Size Lap splicing is not permitted for reinforcement bars larger than 36 mm in diameter. 2. Non-Contact L...
Read more

Pile cap

By -
Image
Pile cap used to transfer the loads from superstructure to the piling. The pile cap is thick concrete mat rests on piles. It is part of the foundation and used to distribute the loads over the piles. Piles used when the soil bearing is not enough to carry loads of the structure. Figure 1  construction management: concrete construction bridge construction:How to become a bridge engineer Pile cap construction procedure Excavation around piles: After 7 days of the casting of the pile the concrete will gain approximately, 70% of it is compressive strength. The soil around piles will be removed to the required levels and dimension that allows construction of the pile cap. A step shall be made if the excavation is more than 1.5 m to prevent soil collapse. Figure 2 Pile head cutting: Concrete will be removed up to cut off level. If concrete under the cut off level is unsound. It shall be removed, and the pile will be repaired...
Read more

stress-strain diagram for aluminium alloy and rubber

By -
Image
figure no:1 showing the stress-strain diagram for aluminum alloy. we can notice from the stress-stress diagram that aluminum has a considerable ductility. despite the absence of explicit yield point as in structural steel . the initial portion of the stress-strain curve is linear with a recognizable proportional limit. the proportional limit for aluminum alloy ranges from 70 to 410 Mpa (10 to 60 Ksi). aluminum alloy undergoes large strain before failure. ultimate stress ranges from 140 to 550 Mpa (20 to 80 Ksi). construction management: concrete construction bridge construction:How to become a bridge engineer Figure-1 Yield stress for aluminum alloy can be determined by drawing offset line parrel to the linear portion of the stress-strain curve. the straight line offset by a standard strain such as 0.002. the intersection point with the stress-strain curve is the point of yield stress. figure no:2 illustrates the concept of offset method. yield stress acquire...
Read more

Non-Working Pile Testing and Static Compression Load Test

By -
Image
Purpose of Non-Working Piles Non-working piles are constructed at the beginning of the project to evaluate soil bearing capacity and determine the maximum settlement. These piles are loaded up to twice the working load. Based on the test results, the pile length may be adjusted. If the measured settlement exceeds the allowable limit, the pile length will be increased accordingly. construction management: concrete construction bridge construction:How to become a bridge engineer Static Compression Load Test The static compression load test provides insight into how the pile responds to loading. Settlement is measured at different load increments to determine the appropriate pile design length. The maximum applied load is typically twice the working load (2 × working load) or as specified by local standards. The following steps outline the testing procedure: A. Steel Cage Preparation The steel reinforcement cage is prepared in accordance with the approved shop drawings. ...
Read more

Repairing of concrete bulging

By -
Image
Improper designing and installation of formwork for a concrete member can result in concrete Bulging. During the placing and compacting of concrete, forms may deflect largely in the weak areas. The deflection of forms will cause concrete to expand at this location, and this known as concrete Bulging. Concrete Bulging will spoil the appearance of a concrete member. Therefore we should always ensure that the forms are appropriately installed, and it is sufficiently supported to resist the concrete during placing and compacting. Bulging should be repaired in case we couldn't avoid it. The solution of concrete Bulging, offset, or surface irregularities are surface grinding. However, excessive surface grinding can weaken the concrete.  Figure 1 If the bulging or surface irregularities are small, grinding of concrete surface will be sufficient to remove surface irregularities. If the Bulging of concrete is significant, then the concrete should be chipped, and the surface...
Read more

Example 5: allowable uniform load can beam support using transformed area method

By -
Image
Using transformed area, what allowable uniform load can this beam support in addition to its own weight for a 28-ft simple span? Concrete weight = 150 lb/ft3 ,fs= 24,000 psi, and fc= 1800 psi. construction management: concrete construction bridge construction:How to become a bridge engineer Figure 1              Transform area=As*n As=1.27*5=6.35in4 Transform area=6.35*8=50.8in2 Location of neutral axis by equalling moment of area around neutral axis as shown in figure 2(assuming neutral axis below the void) X(20)(X/2)-8*8*(x/2-4)=50.8*(29-X) 10X^2-32X+256=1473.2-50.8X 10X^2+18.8X-1217.2=0 X=10.3, assumpitation is not valid Assuming X in void area as shown in figure 3 X(20)(X/2)-8*(X-4)*(x-4)/2=50.8*(29-X) 10X^2-4(X^2-4X-4X+16)-1473.2+50.8X=0 10X^2-4X^2+32X-64-1473.2+50.8X=0 6X^2+82.8X-1409.2=0 X=9.91in now we will calculate moment of inertia using parallel axis theorem  I=2...
Read more

wing wall arrangement and orientation for abutments

By -
Image
wing wall main function is to retain the embankment near abutment. the common slope is 2:1. greater than 2:1 is not allowed. figure no: shows a wing wall for the abutment. Figure 1  there is three arrangement for wing wall: wing wall parallel to abutment: easy to build. construction can be done in a short time. this type of wing wall will not disturb the existing embankment and utilities but it is not the most economical arrangement.   figure 2 construction management: concrete construction bridge construction:How to become a bridge engineer wing wall at an angle with abutments: this type is most economical among the three arrangement. Figure 3 wing wall perpendicular to abutment: in this arrangement. wing wall provides a continuous alignment with bridge deck which can be used to support parapets. this arrangement will disturb existing embankment and utilities adjacent to the structure. for curve bridge, this type o...
Read more

Nominal maximum size of coarse aggregate

By -
Image
Concrete is a widely used material. Reinforced concrete structures can be found everywhere. The main reason behind the popularity of reinforced concrete structure is the high strength and the long life span of these structures. Concrete and steel are combined to produce reinforced concrete. Concrete is good at compression while steel good at tension. Concrete and steel form a perfect combination to resist loads imposed on the structure. Concrete is a composite material composed of cement, coarse aggregate, fine aggregate, and water. Admixtures can be used to enhance concrete properties. A concrete mix consists of almost 65% aggregates. Aggregates are classified into fine and coarse aggregates. Since the aggregates form the majority of a concrete mix. The quality of aggregates can greatly affect the strength and durability of concrete. Aggregates can be natural or crushed aggregates. Used aggregates should be strong, hard, and should not contain a large amount of organic matter or harmf...
Read more

The reasons behind the trimming of pile head

By -
Image
In general, the bored piles are casted to a level higher than the required pile cut-off level. Pile cut-off level is usually similar or a little bit higher than the blinding level of a pile cap. the process of constructing a cast-in-situ pile involves the following steps: installation of the temporary casing to prevent the soil collapse during the drilling process and to guide the drilling rig. Drilling the pile to the required level and diameter. Installation of a reinforcement cage. Reinforcement cage vertical bars will be extended above the pile cut-off level to improve the bonding with the pile cap. The casting of concrete usually done with a tremie pipe. Tremie pipe will be lowered to the bottom of the pile, and then the concrete will be poured. Once the casting is completed, the temporary casing will be removed. It is a common practice to cast the concrete above the cut-off level. the concrete casted then removed for the following reasons: during the casting pro...
Read more