Video from my YouTube channel

Subscribe to My You tube channel

Design of bridge pier

By -


Design brief
The structural member is subdivided into two regions. Region B (BERNOULLI), where the beam theory assumptions are applicable. The main assumptions of beam theory are the cross-section of beam do not deform significantly under applied load, and beam cross-section remains planner and normal to deform axis of the beam. On the other hand, Portions of a structure where the beam theory is not applicable classified as region D. discontinuity, change in section dimension, opening, nodes and connection of girders and beams are examples of D-region.

Members with vary cross-section such as pier cap can be designed using strut and tie method. Strut and tie method is suitable for designing members where beam theory is not applicable. Moreover, it is a conservative method and can be used for the B region. The main concept of the STM method is to represent the flow of internal forces using a truss system consist of strut, ties, and nodes. The modeling of strut and tie is a bit challenging and can vary depends on engineer evaluation and judgment.


Strut and tie method for pier cap
For hammer pier, the cross section of pier change suddenly. This geometric discontinuity will cause a non-linear distribution of strain. Therefore, it is preferred to use STM to design the pier cap. The using of beam theory is not appropriate and can cause discrepancies.

STM modeling
Strut and tie model will be established for a structural member under investigation. The process of modeling can be repeated several times until achieving acceptable geometry of truss and verifying sizes of truss member.

The selection of strut and tie location shall represent the realistic stresses flow from the load to the supports. For figure no:1, the dashed lines represent compression stress trajectories, and the solid lines represent the tension stress trajectories. The representation of these stress identified in figure no:2 the internal compression stress represented by strut (dashed line) and the tension stresses by tie (solid line). In addition to internal stress, the locating of ties should take into consideration the layout and practicality of placing reinforcement steel for a structural member.
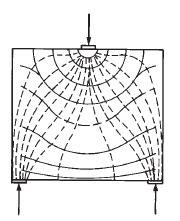Figure 1
Figure 2




The axis of strut shall be located at a distance of a/2 from the edge of the beam in the compression zone. Where a is the depth of a rectangular stress block. Similarly, the ties shall be placed at a distance of a/2  from the edge of the beam in the tension zone.


Figure no:3 showing a strut and tie model for a hammer pier cap. We will analysis the configuration and summarize the points that can assist in designing the STM model.
Figure 3



1. Place the nodes below the loading point and nodes for the reaction at the column. In figure no:3 nodes will be A, C, E, G, I, M, and L.

2. In designing the STM model. The priority should be given for locating strut members. The load will be transferred to the reaction point if the angle with vertical is less than 60 º. In our case, the angle from A to M is more than 60º, so strut cannot be drawn from A to M.

3. The load shall be transferred to a point below bearing location if the angel with vertical between 30º and 60º. In our case, the angle ϕ from A to N is more than 60º, so a new node added at O.

4. For new nodes such as B, the load will be transferred at angle ϕ of 45º approximately. The equilibrium should always be maintained, so a new tie OB is added for node B.

5. Same rules shall be applied for node O. For strut O-M the angles with vertical are more than 60º, so the first rule didn’t apply. Therefore, the load will be transferred to point N. the second rule will be used.

Once the STM modeling completed. The forces for each member of truss shall be calculated. Based on calculated forces, the amount of steel will be calculated. Moreover, the capacity of the strut will be verified.


Design of compression strut


The area of concrete strut should be calculated to determine the nominal resistance of compressive strut. The area of the concrete strut will be controlled by the available concrete area and anchorage condition.


When strut anchored by steel reinforcement. The effective area may be extended to a distance of 6dba beyond anchoring steel where dba is the diameter of anchoring bar. Figure no:4 illustrates the concept of calculating the effective concrete area for the anchored strut.
Figure 4




Figure no:5. Depicting a strut anchored to bearing and tensile reinforcement. For similar condition, the width of the strut can be calculated as shown in the figure.


Figure 5



Calculating the width of strut anchored to bearing plate and other strut represented in the figure no:6


Figure 6



The nominal compressive resistance of strut can be calculated using the following equation [AASHTO 5.6.3.3.1].


Pn=fcu.Acs

Where

Acs is the effective cross-section of a compressive strut.

fcu is limiting compressive stress and can be calculated using the following equation

fcu=fc'/(0.8+170ε1)


ε1=(εs+0.002)*(cot αs)^2


where

fc’ is the concrete compressive strength.

εs is the strain of steel passing through the concrete strut

αs is the smallest angle between concrete strut and tensile tie.

Pu for a strut member shall be always less the Ï•Pn. Where Ï• is a reduction factor equal to 0.7 for compression members [AASHTO 5.5.4.2.1].



Design of tension tie
The reinforcement for tie should be embedded in the nodal zone by a specified embedment length. AASHTO 5.11 specified the requirement for development length. The nominal resistance of tensile tie should be calculated using the following equation [AASHTO 5.6.3.4.1].

Pn=fyAst+Aps[fpe+fs]

Where

fy is the yield strength of longitudinal mild steel for a tie(MPA).

Ast is the total area for longitudinal mild steel for the tie(mm2).

Aps is the area for prestressing steel.

fpe is the effective prestressing force.



ϕPn for tie should be more than Pu (ultimate tensile force at tie). Φ is equal to 0.9, according to AASHTO LRFD. Therefore, a sufficient amount of Ast shall be provided to surpass the ultimate force on the tie.

Vertical ties such as OB and CN should be used to determine shear reinforcement. Number of stirrups can be calculated using the following equation

n=Ast/Astirrup

Two legs or four legs stirrups can be used. The stirrups for OB shall be distributed evenly at L2. Spacing between stirrups can be calculated using the following equation.

S=L2/n

Where

S is the maximum spacing between stirrups.

L2 is the length of the stirrups region.

n is the number of stirrups to comply with Ast.

Design of nodes
AASHTO LRFD limiting the compressive stress at node region according to node region configuration. The limitation can be categorized into:

1. Compressive stress should be less than 0.85 Ï•fc’ for nodes with a strut and bearing area.

2. Compressive stress should be less than 0.75 Ï•fc’ for nodes with tension tie in one-direction only.

3. Compressive stress should be less than 0.65 Ï•fc’ for nodes with tension tie in more than one direction.

There stress in the nodal zone can be reduced by increasing bearing area, strut area, and tie area. In the events of using prestressing for the concrete member. And the stress in the concrete didn’t exceed the effective prestressing force. The limiting compressive stress should be taken as 0.85 Ï•fc’ because the nodal zone didn’t experience any tensile strain.



Pier column design
Column transfers axial loads and resists lateral load imposed on superstructure and column. Shapes of the column section can differ from circular, rectangular, octagonal and others. Slenderness defined as the tendency of the column to buckle. Columns are divided into slender column (tall) and stock column (short).

Columns slenderness
Columns slenderness is an essential factor. The design approach varies depends on the slenderness of columns. Slenderness effects can be evaluated by calculating the slenderness ratio. 

S=(K.lu)/r


Where

K is the effective length factor.

lu is the unsupported length of the compression member

r is the radius of gyration

According to AASHTO 5.7.4.3 if the slenderness ration is more than:

      S=(K.lu)/r≤22 


   S=(K.lu)/r≤34-12 M1/M2for members braced against sway.

Where

M1 is the smaller end moment.

M2 is the larger end moment.

If the slenderness ration is more than the above values and less than 100. Moment shall be magnified according to AASHTO 4.5.3.2.2b. 

According to AASHTO, the factored axial resistance for compression member subjected to pure compression can be calculated using the following equation.

1.For a member with spiral reinforcement

Pn=0.85Ï•fc'(Ag-Ast)+fy.Ast


2.For a member with tie reinforcement

Pn=0.80Ï•fc' (Ag-Ast)+fy.Ast



Where

Φ is the resistance factor in AASHTO 5.5.4.2

fc’ is the concrete strength at 28 days

Ag is the cross-section area for compression member (mm2)

Ast is the area of longitudinal reinforcement(mm2)

fy is the yield stress of reinforcement steel(MPA)





Reduced nominal compression resistance should always be larger than applied ultimate load


Ï•Pn≥Pu




Biaxial flexural
It is rare for a column to be loaded with pure compression only with no bending moment. The bending moment can be generated due to continuity in structure spans. Transverse loads, temperature change, concrete shrinkage, and creep will induce bending stresses on columns. According to AASHTO5.7.4.5, the axial resistance can be calculated for column subjected to axial load with eccentricity in both direction and axial load with bending moment using the following equation.



If factored axial load  Pu≥0.1Ï•fc' Ag

1/Prxy=1/Prx+1/Pry-1/Ï•Po



Where

Po=0.85fc' (Ag-Ast)+fyAst



If factored load    Pu>0.1Ï•fc'Ag


Mux/Mrx+Muy/Mry≤1

Where

Prxy is factored axial resistance in biaxial flexure.

Prx is factored axial resistance based on the assumption of ey is present only

Pry is factored axial resistance based on the assumption of ex is present only

Pu is factored applied axial load.

Mux is factored applied moment about the x-axis

Muy is factored applied moment about the y-axis

Mrx = uniaxial factored flexural resistance of a section about x-axis corresponding to the eccentricity produced by the applied factored axial load and moment.

Mry = uniaxial factored flexural resistance of a section about y-axis corresponding to the eccentricity produced by the applied

factored axial load and moment


The uniaxial resistance (Prx,Pry,Mrx,Mry) can be calculated using the column design chart. Column design charts as in figure no:7 will help in reducing time and simplifying the complexity of designing biaxial flexural column. Uniaxial resistance will be calculated for each direction then used in the previous equation to calculate biaxial resistance of the column.
Figure 7

Comments

Post a Comment

Videos from My Youtube channel

Popular posts from this blog

Pile cap

By -
Image
Pile cap used to transfer the loads from superstructure to the piling. The pile cap is thick concrete mat rests on piles. It is part of the foundation and used to distribute the loads over the piles. Piles used when the soil bearing is not enough to carry loads of the structure. Figure 1  construction management: concrete construction bridge construction:How to become a bridge engineer Pile cap construction procedure Excavation around piles: After 7 days of the casting of the pile the concrete will gain approximately, 70% of it is compressive strength. The soil around piles will be removed to the required levels and dimension that allows construction of the pile cap. A step shall be made if the excavation is more than 1.5 m to prevent soil collapse. Figure 2 Pile head cutting: Concrete will be removed up to cut off level. If concrete under the cut off level is unsound. It shall be removed, and the pile will be repaired...
Read more

Bridge Diaphragm

By -
Image
The main function of diaphragms is to provide a stiffening effect to deck slab in case bridge webs are not situated directly on top of bearings. Therefore, diaphragms may not be necessary in case bridge bearings are placed directly under the webs because loads in bridge decks can be directly transferred to the bearings.On the other hand, diaphragms also help to improve the load-sharing characteristics of bridges. Diaphragms also contribute to the provision of torsional restraint to the bridge deck. Diaphragm will be used also to resist stresses that occurs during the post-tensioning process. Post-tensioning hardware are casted inside the diaphragm. Figure 1 construction management: concrete construction bridge construction:How to become a bridge engineer Types of diaphragm: Diaphragm at the span end: this type of diaphragms will be located between two bridge spans or at the bridge abutments. Expansion joints will be used to connect bridge spans. This ...
Read more

Binding wire for steel reinforcement

By -
Image
  Binding wires are used to tie steel bars together. These wires are playing a significant role in maintaining the reinforcement stability and rigidity. Wires are used to tie the steel bars at intersections points. By tying the steel bars together, we ensure that the steel bars will not move from their locations during construction or during the time of concreting. In slabs, binding wires are used to tie longitudinal and transverse bars together. In columns, it is used to tie vertical bars with stirrups.   Figure 1 There are various types of binding wires such as  Black annealed baling wire, Stainless Steel Binding Wire, and PVC coated binding wires.  Black annealed baling wire used to tie black steel. The popular size for black wire ranges from 16 to 22 gauges. Stainless steel binding wires are used to bind stainless steel reinforcement. Stainless steel reinforcement is used in a harsh environment where the black steel gets rusted quickly. Therefore, stainless ...
Read more

stress-strain diagram for aluminium alloy and rubber

By -
Image
figure no:1 showing the stress-strain diagram for aluminum alloy. we can notice from the stress-stress diagram that aluminum has a considerable ductility. despite the absence of explicit yield point as in structural steel . the initial portion of the stress-strain curve is linear with a recognizable proportional limit. the proportional limit for aluminum alloy ranges from 70 to 410 Mpa (10 to 60 Ksi). aluminum alloy undergoes large strain before failure. ultimate stress ranges from 140 to 550 Mpa (20 to 80 Ksi). construction management: concrete construction bridge construction:How to become a bridge engineer Figure-1 Yield stress for aluminum alloy can be determined by drawing offset line parrel to the linear portion of the stress-strain curve. the straight line offset by a standard strain such as 0.002. the intersection point with the stress-strain curve is the point of yield stress. figure no:2 illustrates the concept of offset method. yield stress acquire...
Read more

Chamfers for concrete structures

By -
Image
In general, the edges of concrete members are chamfered. Usually during the process of installing forms for a structural member such as pile cap, a chamfer a PVC chamfer as shown in figure no:1 installed at the edges of the structural members. These chamfers will form smooth slanted edges, as shown in figure no:2. The size of chamfers can be 20x20mm or more as shown on the contract drawing. The PVC chamfer fixed to forms by nails. We should ensure that the PVC chamfer fixed in their correct locations, and we should ensure that the PVC chamfer is straight and not moving up or down. Checking the alignment and location of PVC chamfer is important, so the chamfered concrete edge will have a good appearance after the form’s removal.  Figure 1 Figure 2 Chamfering the concrete edges done for many reasons such as aesthetics, some suggesting that the chamfering of concrete edges done for safety to reduce the damage of objects due to impact with sharp concrete edges. Actually, ...
Read more

Non-Working Pile Testing and Static Compression Load Test

By -
Image
Purpose of Non-Working Piles Non-working piles are constructed at the beginning of the project to evaluate soil bearing capacity and determine the maximum settlement. These piles are loaded up to twice the working load. Based on the test results, the pile length may be adjusted. If the measured settlement exceeds the allowable limit, the pile length will be increased accordingly. construction management: concrete construction bridge construction:How to become a bridge engineer Static Compression Load Test The static compression load test provides insight into how the pile responds to loading. Settlement is measured at different load increments to determine the appropriate pile design length. The maximum applied load is typically twice the working load (2 × working load) or as specified by local standards. The following steps outline the testing procedure: A. Steel Cage Preparation The steel reinforcement cage is prepared in accordance with the approved shop drawings. ...
Read more

Elastomeric expansion joint

By -
Image
Elastomeric expansion joints can accommodate a wide range of movement 30-800 mm, and it can easily installed and provide a smooth ride with minimal noise and vibration. It can be found in different formats. Each format accommodates different type of movement. Figure 1 Elastomeric joints consist of reinforced neoprene. Steel plates shall be embedded in the neoprene molded section to meet the structural requirement. Figure no:2 shows elastomeric expansion joint different components. construction management: concrete construction bridge construction:How to become a bridge engineer Figure 2 The elastomeric joint shall be skid resistance, armored and it should provide  smooth riding, and it shall be durable.  Installation of joint shall be strict accordance to specification and manufacturer recommendation.  construction management: concrete construction bridge construction:How to become a bridge engineer Ins...
Read more

Repairing of concrete bulging

By -
Image
Improper designing and installation of formwork for a concrete member can result in concrete Bulging. During the placing and compacting of concrete, forms may deflect largely in the weak areas. The deflection of forms will cause concrete to expand at this location, and this known as concrete Bulging. Concrete Bulging will spoil the appearance of a concrete member. Therefore we should always ensure that the forms are appropriately installed, and it is sufficiently supported to resist the concrete during placing and compacting. Bulging should be repaired in case we couldn't avoid it. The solution of concrete Bulging, offset, or surface irregularities are surface grinding. However, excessive surface grinding can weaken the concrete.  Figure 1 If the bulging or surface irregularities are small, grinding of concrete surface will be sufficient to remove surface irregularities. If the Bulging of concrete is significant, then the concrete should be chipped, and the surface...
Read more

Structural design of road pavement

By -
Image
  Designing efficient and durable roads starts with understanding one key factor: traffic. Traffic analysis provides engineers with essential data that directly influences decisions about road width, pavement thickness, and overall design. In this blog, we’ll walk through the fundamental steps of traffic analysis, from traffic surveys to axle load studies, and how each component contributes to building roads that last. watch the full course from here 1. Traffic Analysis The amount and type of traffic a road will carry play a crucial role in pavement design. Roads with heavier traffic flows require not only wider carriageways but also thicker pavements to withstand the higher load repetitions. To estimate how much load a road will bear over its design life, engineers need to conduct a traffic survey . This survey helps assess current traffic volumes and project future trends, giving us a clearer picture of what the pavement needs to endure. 1.1 Traffic Surveys: Gat...
Read more

Balanced section, tension controlled section and compression controlled section of reinforced concrete beams

By -
Image
RC beams where reinforcing steel yields at the same time in which concrete strain at extreme compression fiber is 0.003(concrete reach it is flexural capacity at this value of strain) called balanced section. Figure 1 construction management: concrete construction bridge construction:How to become a bridge engineer in compression controlled section the strain at extreme fiber for concrete reached 0.003 before steel yield. in this case, the section is over reinforced. for compression controlled section slight and unnoticeable deflections will occur to RC beams. this will result in a sudden failure without any warning in case of overloading. these members called as brittle members and it should be avoided.                               Figure 2 in tension controlled members. reinforcing steel yields before the concrete strain at extreme compression fiber reaches 0.003. in this ty...
Read more